Semester 3 - Data Structure & Algorithm

Trees

• Trees are hierarchical structures with a root node and connected nodes without cycles.
• Each node has a parent (except root) and children.
• Leaf nodes have no children.
• Depth: number of edges from root to node
• Height: number of edges from node to deepest leaf.
• Trees have various applications:
  • File system in OS
  • B-Tree, B+-Tree for indexing in databases
  • Syntax Tree in compilers
  • Document Object Model (DOM)

Binary Trees

• Binary trees are trees where each node has up to two children: left and right.
• Types include:
  • Full: Nodes have 0 or 2 children.
  • Perfect: All nodes have two children, leaves are at the same level.
  • Complete: All levels are fully filled except possibly the last.
  • Balanced: Left and right subtrees’ heights differ by at most one.
  • Degenerate: Each node has only one child, similar to a linked list.

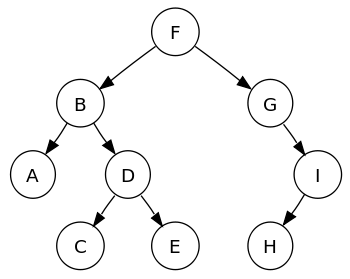
Binart Tree

Binary Search Trees (BST)

• BST is a binary tree where each node’s left children are less than the node and right children are greater.
• Operations:
  • Search: Traverse from root to left/right subtree based on comparison until value is found or subtree is null.
  • Insertion: Like search, but create a new node at null subtree.
  • Deletion: Remove node and maintain BST property. Consider cases: no child, one child, two children.

BST - Insert Operation

AVL Trees

• Named after inventors Adelson-Velsky and Landis
• Self-balancing binary search trees.
• Heights of two child subtrees of any node differ by at most one.
• Rebalancing is done through rotations if heights differ by more than one.
• Offer faster retrievals but slower insertions and deletions compared to some other trees.
• Used in applications where fast retrievals are crucial.

Balance Factor

• Balance factor (k) = height of left sub-tree - height of right sub-tree.
• Balance factor 1: left sub-tree is one level higher.
• Balance factor 0: both sub-trees are of equal height.
• Balance factor -1: right sub-tree is one level higher.
• An AVL tree has balance factors within the range -1 to +1.

AVL Trees Rotations

• AVL Tree Rotations: Performed to maintain balance during insertions/deletions.
• Four types: Left-Left, Right-Right, Left-Right, Right-Left.
• Left-Left (LL): Single right rotation.
• Right-Right (RR): Single left rotation.
• Left-Right (LR): Double rotation; first left, then right.
• Right-Left (RL): Double rotation; first right, then left.
• Rotations restore balance without affecting order properties.

AVL Trees - Rotations Animation

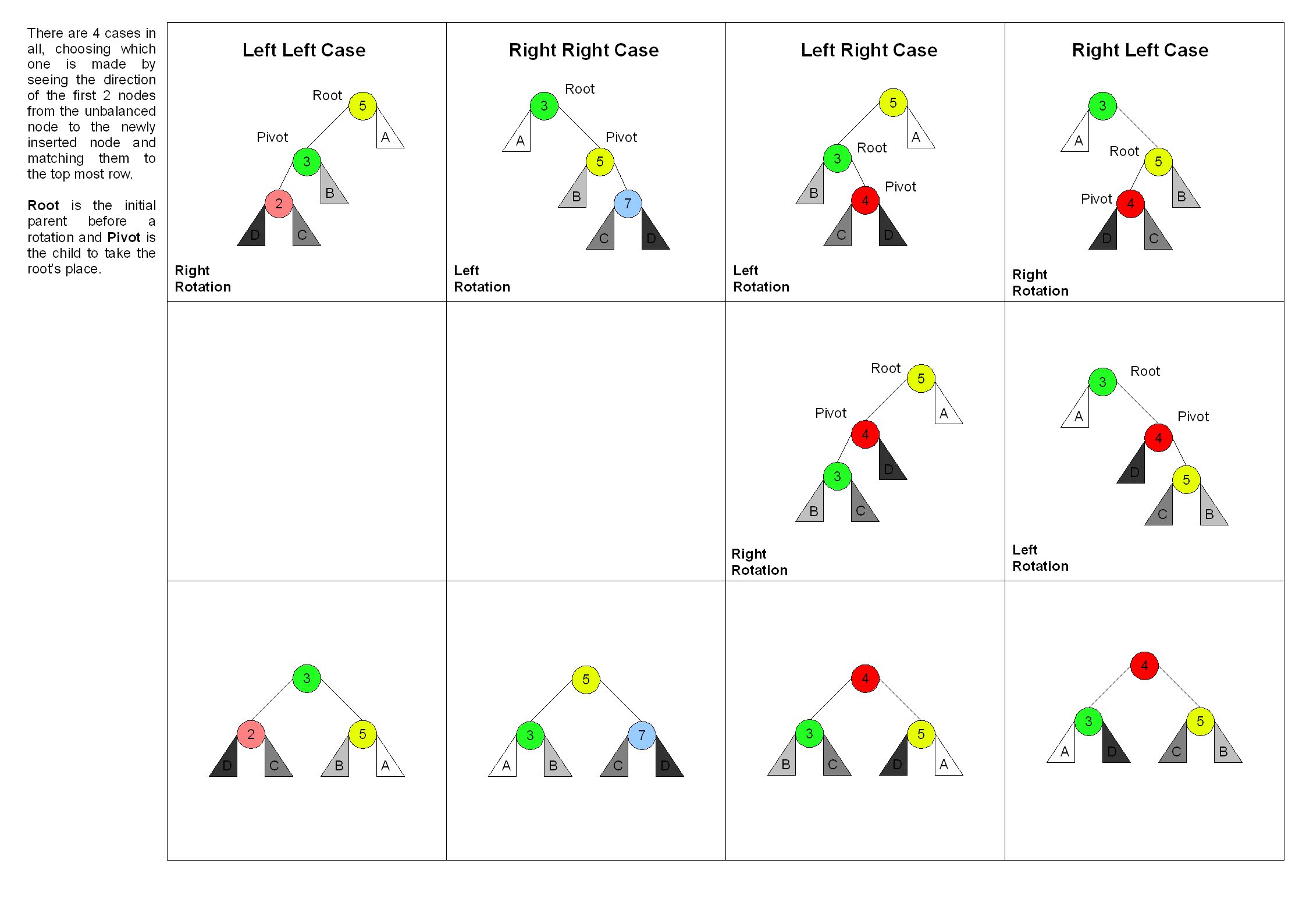AVL Trees - Rotations

Tree traversal

• Process of visiting each node in a tree once.
• Can be depth-first (In-order, Pre-order, Post-order) or breadth-first.
• There are three common ways to traverse a tree in depth-first order:
  • In-order (Left, Root, Right)
  • Pre-order (Root, Left, Right)
  • Post-order (Left, Right, Root)

In-order Traversal

Pre-order Traversal

Post-order Traversal