Week 11-13 - Graph Theory - Basics

Graph Theory

A graph (G = {V, E}) consists of a set of vertices (V) and a set of edges (E) that connect them.

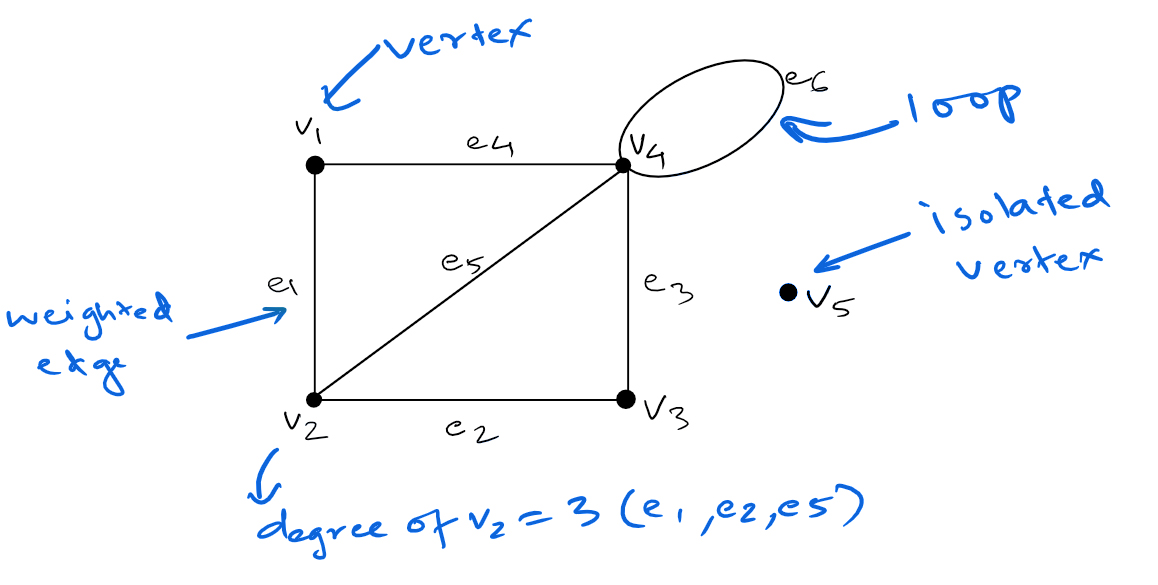
• Vertex: A point or node in a graph.
• Edge: A connection between two vertices in a graph.
• Isolated Vertex: A vertex with 0 degree, meaning it’s not an endpoint of any edge.
• Degree of a Vertex: The number of edges connecting to a vertex.
• Walk: A sequence of vertices and edges in a graph.
  • Closed Walk: A walk that ends with the same vertex, also known as a cycle.
  • Open Walk: A walk that starts and ends with different vertices.
• Path: A walk with neither edges nor vertices repeating.
• Trail: A walk with no repeated edges.
• Circuit: A closed walk where no edge is allowed to repeat but vertices can repeat.
• Loop: An edge that connects a vertex to itself.
• Directed Graph: A graph where edges have a direction.

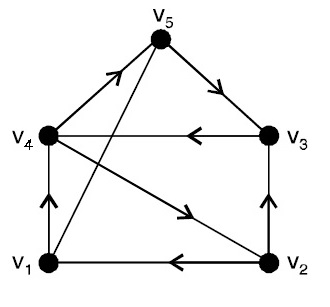Directed Graph

• Weighted Graph: A graph where edges have a numerical value called weight.
• Complete Graph: A graph where every pair of vertices is connected by an edge.

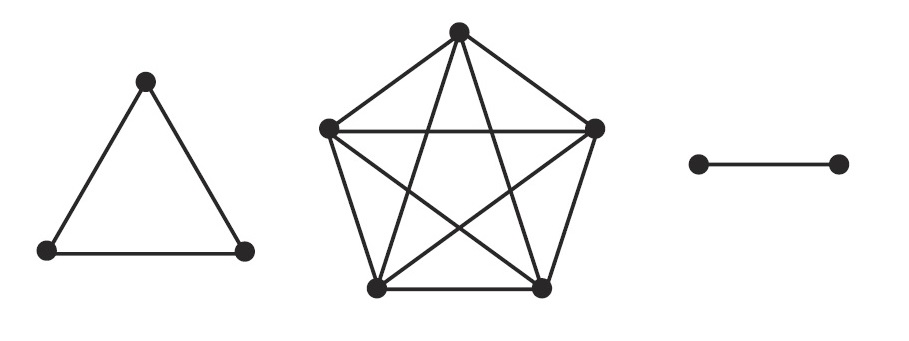Complete Graphs

• Connected Graph: A graph where there is a path between every pair of vertices.

Connected Graphs

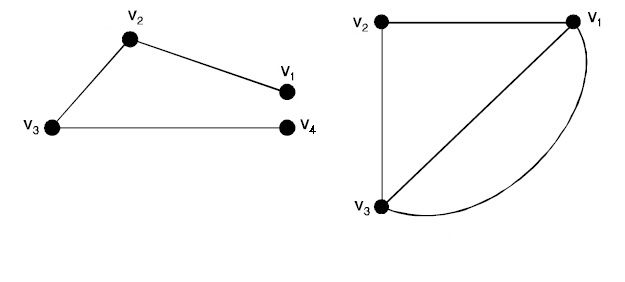
• Disconnected Graph: A graph with one or more components that are not connected to others.

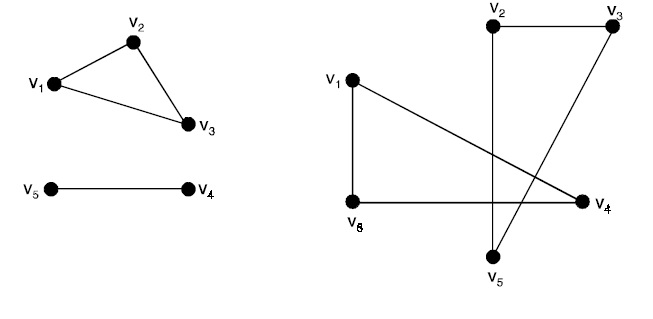Disconnected Graphs

• Acyclic Graph: A graph without cycles.
• Tree: A connected acyclic graph.
• Isomorphism: Two graphs are isomorphic if they have the same structure, meaning their vertices and edges can be matched in a way that preserves adjacency relationships.
  • The two isomorphic graphs must have
    • the same number of vertices,
    • the same number of edges, and
    • an equal number of vertices with a same degree sequence.
    • If a cycle of length k is formed by the vertices { v1 , v2 , ….. , vk } in one graph, then a cycle of same length k must be formed by the vertices { f(v1) , f(v2) , ….. , f(vk) } in the other graph as well.

In other words, two graphs are isomorphic if there exists a mapping from one vertex set to another that preserves adjacency/structure.

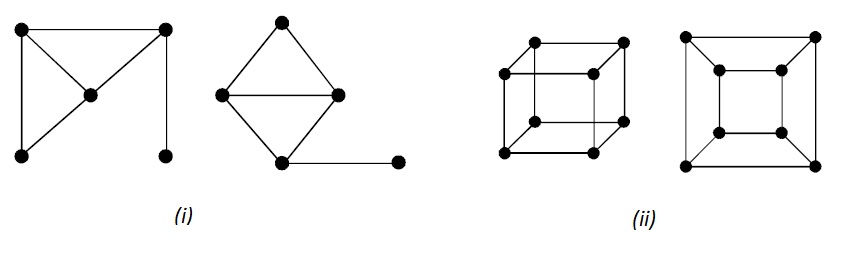Isomorphic graphs

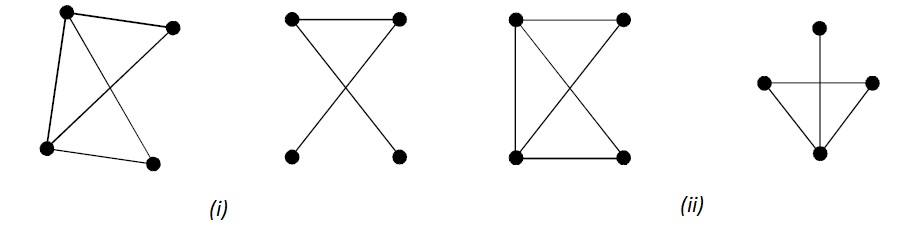These graphs are not Isomorphic

• Euler Graph: A graph which has a Eulerian circuit is called an Eulerian graph.
  • Euler Path: It is called Euler path if it includes every edges exactly once.
  • Euler Circuit: An Euler path that is a circuit is called Euler circuit.

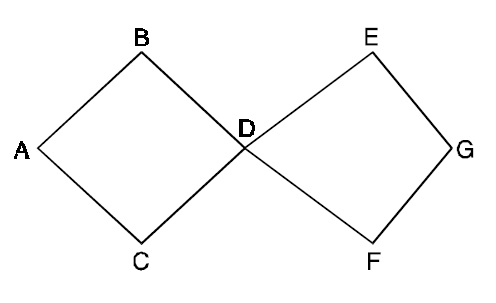Euler Graph (ABDEGFDCA is an Euler path and circuit. All vertices of even degree.)

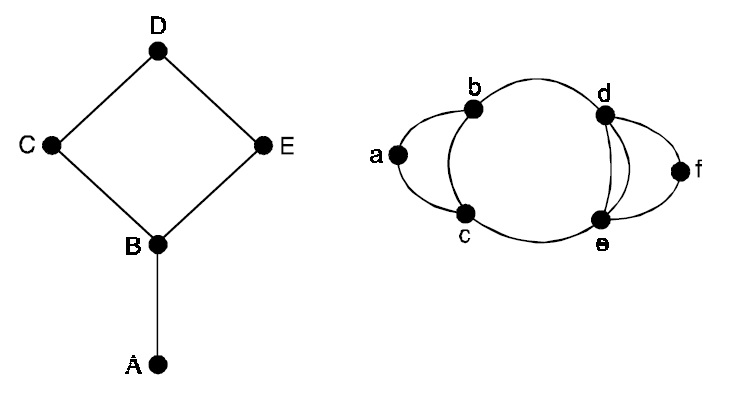In left, ABCDEB and BCDEBA are two Euler paths. Starting from any vertex no Euler circuit can be found. On right, no Euler path and circuit is possible. All vertices are not even degree and more than two vertices are of odd degree.

TIP :
To determine whether a graph G has an Euler circuit:
(i) List the degree of all vertices in the graph.
(ii) If any value is zero, the graph is not connected and hence it cannot have Euler path or Euler circuit.
(iii) If all the degrees are even, then G has both Euler path and Euler circuit.
(iv) If exactly two vertices are odd degree, then G has Euler path but no Euler circuit.

• Hamiltonian Graph: A graph that has a path (known as a Hamiltonian circuit) which visits every vertex exactly once.

To not get confused:

• Eulerian: circuit is a closed path that visits every edge of a graph exactly once
• Hamiltonian: circuit is a closed path that visits every node of a graph exactly once.

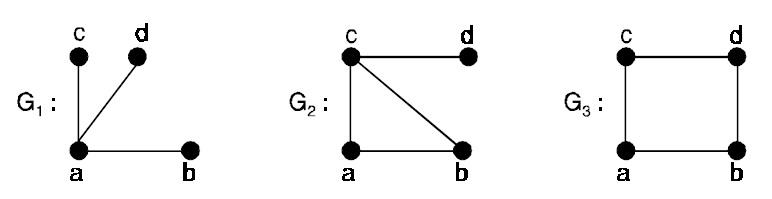
G1 has no hamiltonian path (and so hamiltonian cycle), G2 has hamiltonian path abcd but no hamiltonian cycle, while G3 has hamiltonian cycle abdca.

And let’s revise all the sequences,

Type	Repeated vertices?	Repeated edges?	Open or Closed?
Walk	Yes	Yes	Both
Trail	Yes	No	Open
Path	No	No	Open
Circuit	Yes	No	Closed
Cycle	No	No	Closed

NOTE :
For closed sequences, start and end vertices are the only ones that can repeat.
Every cycle is a circuit, but the contrary is not true.

• Bipartite Graph: Vertices divided into two sets with edges between them such that vertices in the same set can be adjacent.

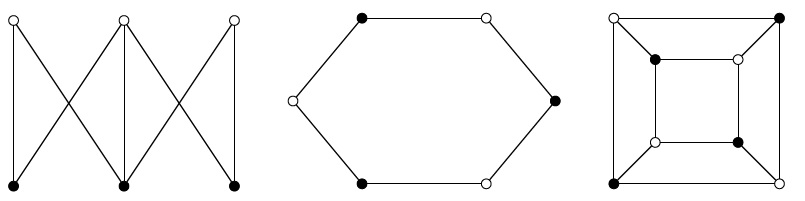
Examples of Bipartite graphs, showing two sets of white and black vertices. No vertex is adjacent to other vertex in the same set.

• Complete Bipartite Graph: Every vertex of one set is adjacent to every vertex of the other.

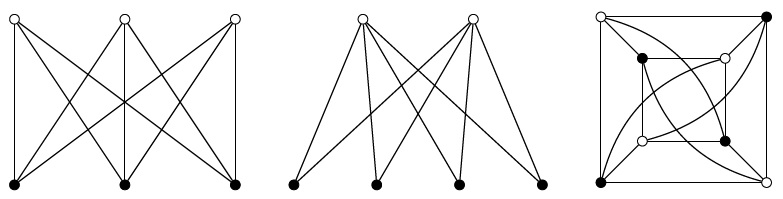
Examples of Complete Bipartite graphs, showing two sets of white and black vertices. Every vertex from one set is connected to every vertex in an other.

• Cut Vertex: A vertex whose removal disconnects the graph into multiple components.

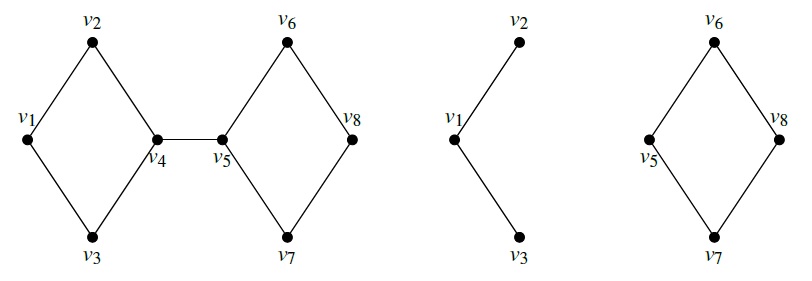
Connected graph on left. On right, vertex v4 being the cut vertex, disconnected the graph by taking out 3 edges.

• Subgraph: A subset of the vertices and edges of a larger graph.
• Spanning Subgraph: A subgraph with all original graph vertices.

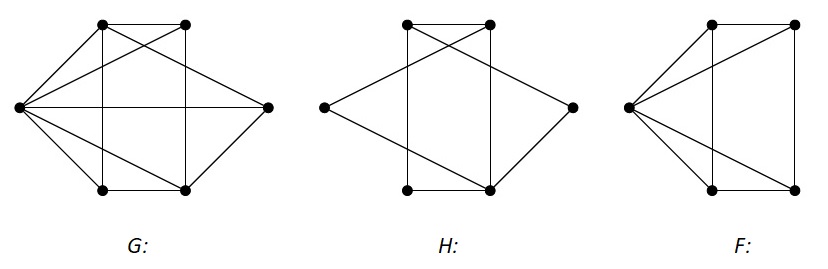
Graph H is the Spanning subgraph of graph G and F is a subgraph of graph G

• Induced Subgraph: A subgraph containing all edges between vertices in a subset.

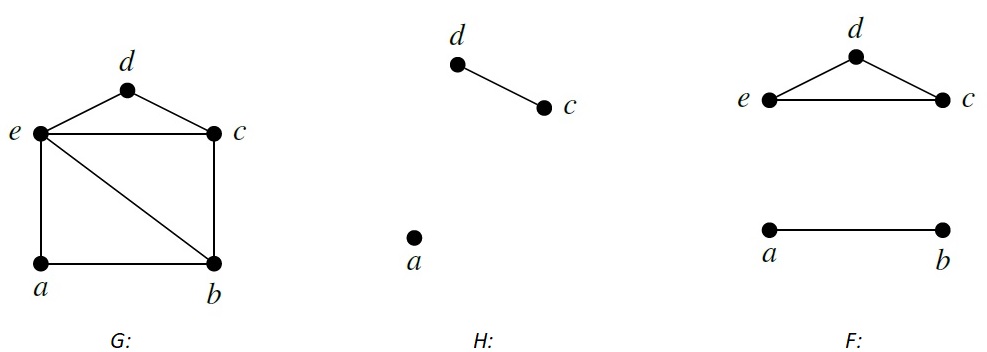
Graph H[a,c,d] is Induced subgraph of G with vertices and Graph F[ab,cd,de,ce] is Edge Induced subgraph of G.

Matrix

Unfortunately no one can be told what the Matrix is. You have to see it for yourself.
— Morpheus, The Matrix

• Adjacency Lists: A list of vertices and their adjacent vertices used to represent a graph.
• Adjacency Matrix: A matrix with rows and columns representing vertices and a 1 indicating an edge between them.

Adjacency list and matrix representation of a graph (left - graph, centre - list representation view, right - matrix)

• Incidence Matrix: A matrix with rows representing vertices and columns representing edges, with entries indicating vertex-edge incidence.

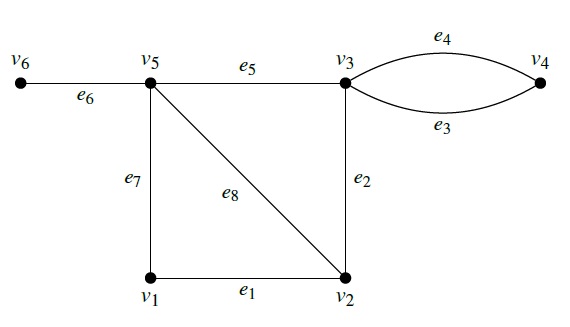
A Graph G

Incidence list representation of graph G

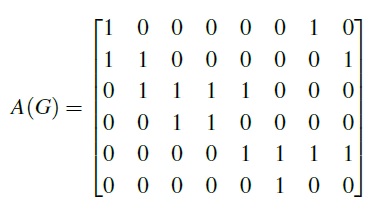
Matrix of graph G

1. Since every edge is incident on exactly two vertices, each column of A has exactly two ones.
2. The number of ones in each row equals the degree of the corresponding vertex.
3. A row with all zeros represents an isolated vertex.
4. Parallel edges in a graph will have identical columns.

TIP: Adjacency matrix of isomorphic graphs are identical. Hence, it can be used to check isomorphism.