Week 4 - Set-Theory
3 minute read
1. Set Theory
- Collection of distinct objects
- Union, intersection, and difference operations
- Example: A = {1, 2, 3}, B = {2, 3, 4}, A ∪ B = {1, 2, 3, 4}
2. Automata Theory
- Abstract machines, like finite automata, which can be used to model and analyze the behavior of systems
- Example: a simple vending machine that accepts only coins and dispenses a soda
3. Probability
- Likelihood of an event occurring
- P(A) = (favorable outcomes) / (total possible outcomes)
- Example: Probability of rolling a 6 on a fair die: P(6) = 1/6
4. Linear Algebra
- Study of vectors, matrices, and linear equations
- Solving systems of linear equations using matrices
- Example: Matrix multiplication, eigenvalues, and eigenvectors
5. Graph
- Collection of nodes (vertices) and edges
- Directed or undirected
- Example: Social networks, web pages, road networks
6. Subset Sum Problem
- Determine if there exists a subset of given numbers that sum to a target value
- Example: S = {1, 2, 3, 4}, target = 5, solution = {1, 4}
7. Apriori Algorithm
- Identify frequent itemsets for association rule mining
- Example: Market basket analysis, finding frequent itemsets in sales data
- Measure of the reduction in uncertainty after splitting a dataset
- Used in decision tree algorithms
- Example: Selecting the best attribute to split a dataset in a decision tree
- Example 2:
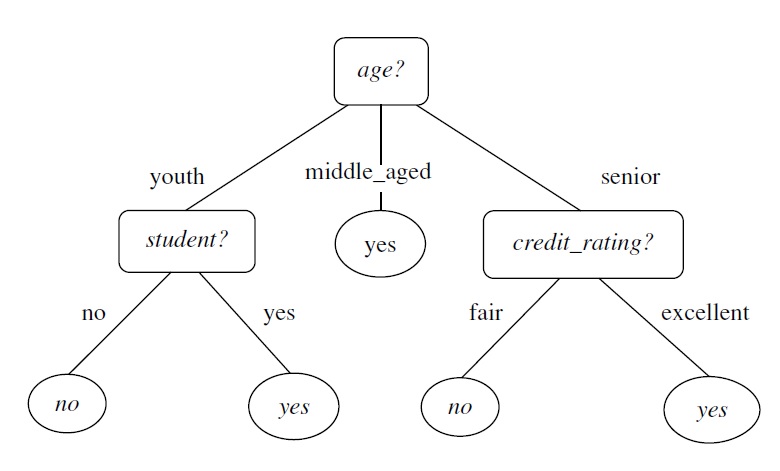
10. Notations - Set Theory
- Set:
Collection of distinct elements, denoted by uppercase letters (A, B, C)
- Element:
Individual items within a set, represented by lowercase letters (a, b, c)
- Membership notation:
a ∈ A (a is an element of set A)
- Not a member notation:
a ∉ B (a is not an element of set B)
- Subset:
All elements of A are in B, denoted A ⊆ B
- Proper subset:
Subset not equal to the original set, denoted A ⊂ B
- Superset:
Set A contains all elements of set B, denoted A ⊇ B
- Universal set:
Contains all elements under consideration, denoted U or Ω
- Empty set (Null set):
Set with no elements, denoted ∅ or {}
- Intersection:
Set of elements common to A and B, denoted A ∩ B
- Union:
Set of all elements in A and B, denoted A ∪ B
- Difference:
Set of elements in A but not in B, denoted A - B or A \ B
- Complement:
Set of elements in universal set U but not in A, denoted A' or A^c
- Cardinality:
Number of elements in a set, denoted |A|
- Power set:
Set of all subsets of A, including empty set and A itself, denoted P(A) or 2^A
11. Specifying Sets
- Listing method:
Enumerate elements, e.g., A = {1, 2, 3}
- Set-builder notation:
Define by properties, e.g., B = {x | x > 0, x ∈ Z}
- Characteristic function:
Indicator function, e.g.,𝜒_A(x) = 1 if x ∈ A, 0 otherwise
- Recursive formula:
Define via recursion, e.g., Fibonacci sequence: F(0) = 0, F(1) = 1, F(n) = F(n-1) + F(n-2)
12. Types of Sets
- Null set: {}
- Singleton set: {1}
- Finite set: {1, 2, 3}
- Infinite set: N (natural numbers)
- Equivalent sets: same number of elements
- Equal sets: same elements
- Subset: A ⊆ B
- Superset: A ⊇ B
- Universal set: U
- Power set: P(A), set of all subsets of A
13. Venn Diagram and Set Operations
- Venn Diagram: Visual representation of sets and their relationships
- Set operations: Union, intersection, difference, and complement
14. Venn Diagram - Example
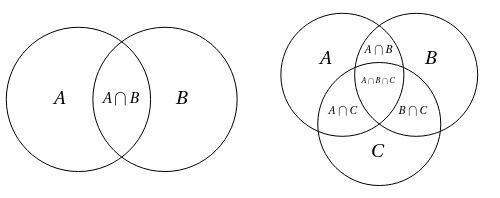
15. Venn Diagram - Subset and Superset
- Subset: Set A is a subset of B if all elements of A are also in B
- Superset: Set A is a superset of B if A contains all elements of B
16. Set Operations
- Union: A ∪ B, all elements in either A or B
- Intersection: A ∩ B, all elements in both A and B
- Difference: A - B, all elements in A but not in B
17 Venn Diagram Applications
- Various applications of Venn diagrams in research and analysis like
- Bioinformatics (gene overlaps, protein interactions)
- Social network analysis (shared connections)
- Market segmentation (customer overlap)
- Visualizing relationships, intersections, and unions
Attributions





