Week 10 - Number Theory - Applications

Cryptography Basics

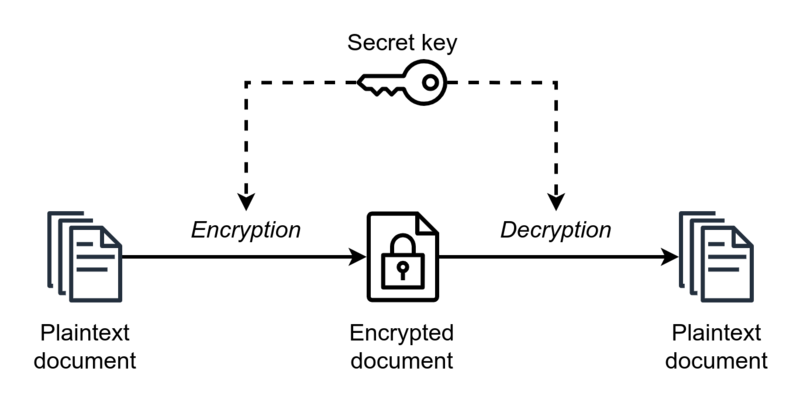
• Cryptography: Science of securing communication through secret codes.
• Encryption: Converting plaintext to unreadable ciphertext using a secret key.
• Decryption: Converting ciphertext back to plaintext using the same or a corresponding key.

Symmetric Cipher Model

• Uses the same key for encryption and decryption.
  Example ¹

Caesar Cipher

• Simple substitution cipher that shifts letters by a fixed number.
• Example: “HELLO” shifted by 3 becomes “KHOOR”.
  • H -> K (shifted 3 positions)
  • E -> H (shifted 3 positions)
  • L -> O (shifted 3 positions)
  • L -> O (shifted 3 positions)
  • O -> R (shifted 3 positions)

C: Cipher text
p: Plain text
k: Key (shift value)

Encryption formula:
C = (p + k) mod 26

Decryption formula:
p = (C - k) mod 26

Reference chart:

Affine Cipher

• Combination of Caesar cipher and multiplication.
• 312 possible keys
• Example: “HELLO” with a = 5 and b = 8 becomes “ZEBBY”.
  • H -> Z (5 * 7 + 8) mod 26 = 25
  • E -> E (5 * 4 + 8) mod 26 = 4
  • L -> B (5 * 11 + 8) mod 26 = 1
  • L -> B (5 * 11 + 8) mod 26 = 1
  • O -> Y (5 * 14 + 8) mod 26 = 24

E(x): Encryption function
D(y): Decryption function
x: Plain text
y: Cipher text
a, b: Key values

Encryption formula:
y = (ax + b) mod 26

Decryption formula:
x = a⁻¹(y - b) mod 26

Vigenere Ciphers

• Polyalphabetic (multiple) substitution cipher.
• Uses a keyword to determine the shift for each character.
• Example: “HELLO” with keyword “KEY” becomes “RIJVS”.
  • H -> R (shifted by 10 positions as per K)
  • E -> I (shifted by 4 positions as per E)
  • L -> J (shifted by 24 positions as per Y)
  • L -> V (shifted by 10 positions as per K)
  • O -> S (shifted by 4 positions as per E)

Instead of keyword, you might be given a number as a key.

Transposition Cipher

• Rearranges the order of characters in the plaintext.

Example:
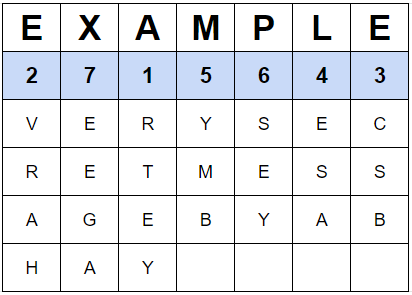
Plaintext: VERY SECRET MESSAGE BY ABHAY
Keyword/phrase: EXAMPLE

• Steps

  • write down the keyword at top
  • assign number to each letter based on alphabetical order
  • if a letter repeats (like “E” in our case), second occurrence is treated as the next letter in alphabetical order.
  • write plaintext in rows irrespective of how ugly they look.
  • create cypher tex by reading columns in assigned numbers (1 to 7)

Cypher text: "RTEY VRAH CSB ESA YMB SEY EEGA"

Rail Fence Cipher

• Example: “HELLO” with 3 rails becomes “HOELL”.
  • Write “HELLO” in a zigzag pattern with 3 rails:

      H . . . O
      . E . L .
      . . L . .
    

  • Read horizontally: “HOELL”

Frequency Analysis

• Analyzing the frequency of characters in ciphertext to decrypt the message.

Asymmetric Cryptosystem

RSA (Rivest-Shamir-Adleman Algorithm)

• Developed by: Ronald Rivest, Adi Shamir, Leonard Adleman
• RSA is an asymmetric cryptosystem, meaning it uses separate keys for encryption and decryption.
• widely used

Steps to generate keys:

1. Choose two large prime numbers p and q.
2. Calculate n = p × q.
3. Calculate the quotient function φ(n) = (p - 1) × (q - 1).
4. Choose an integer e, such that 1 < e < φ(n) and gcd(φ(n), e) = 1 (e and φ(n) are relatively prime).
5. Calculate the integer d, such that d × e ≡ 1 (mod φ(n)).
6. The public key is {e, n}.
7. The private key is {d, n}.

Encryption and Decryption:

• Encryption: Ciphertext (C) = Message (M)^e mod n
• Decryption: Message (M) = Ciphertext (C)^d mod n

Example:

1. Choose primes p = 3 and q = 11.
2. Compute n = 3 × 11 = 33.
3. Compute φ(n) = (3 - 1) × (11 - 1) = 20.
4. Choose e = 3, such that gcd(20, 3) = 1.
5. Compute d = 7, such that d × e ≡ 1 (mod φ(n)).
6. Public key: {e = 3, n = 33}.
7. Private key: {d = 7, n = 33}.

Encryption: Message (M) = 7 Ciphertext (C) = (7^3) mod 33 = 13

Decryption: Ciphertext (C) = 13 Message (M) = (13^7) mod 33 = 7

Attributions:

1. MarcT0K (icons by JGraph), CC BY-SA 4.0, via Wikimedia Commons ↩